About Bayesian Optimization
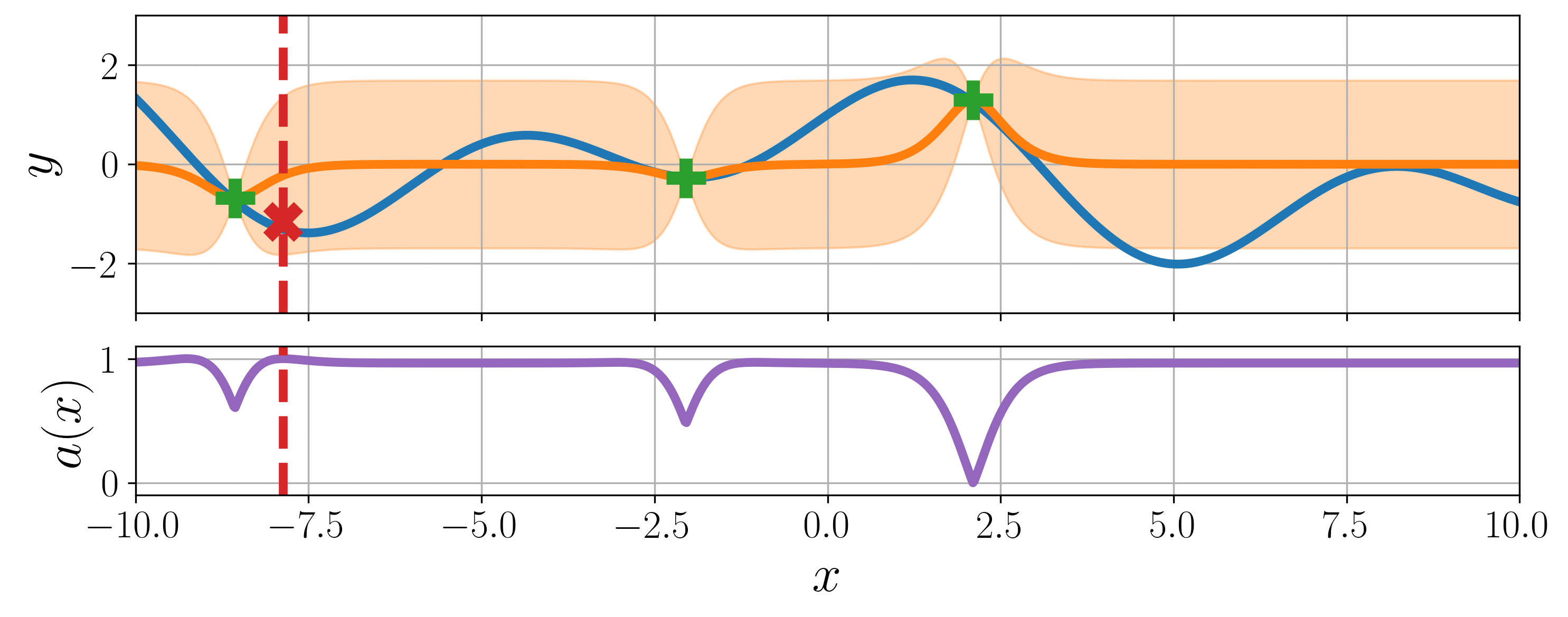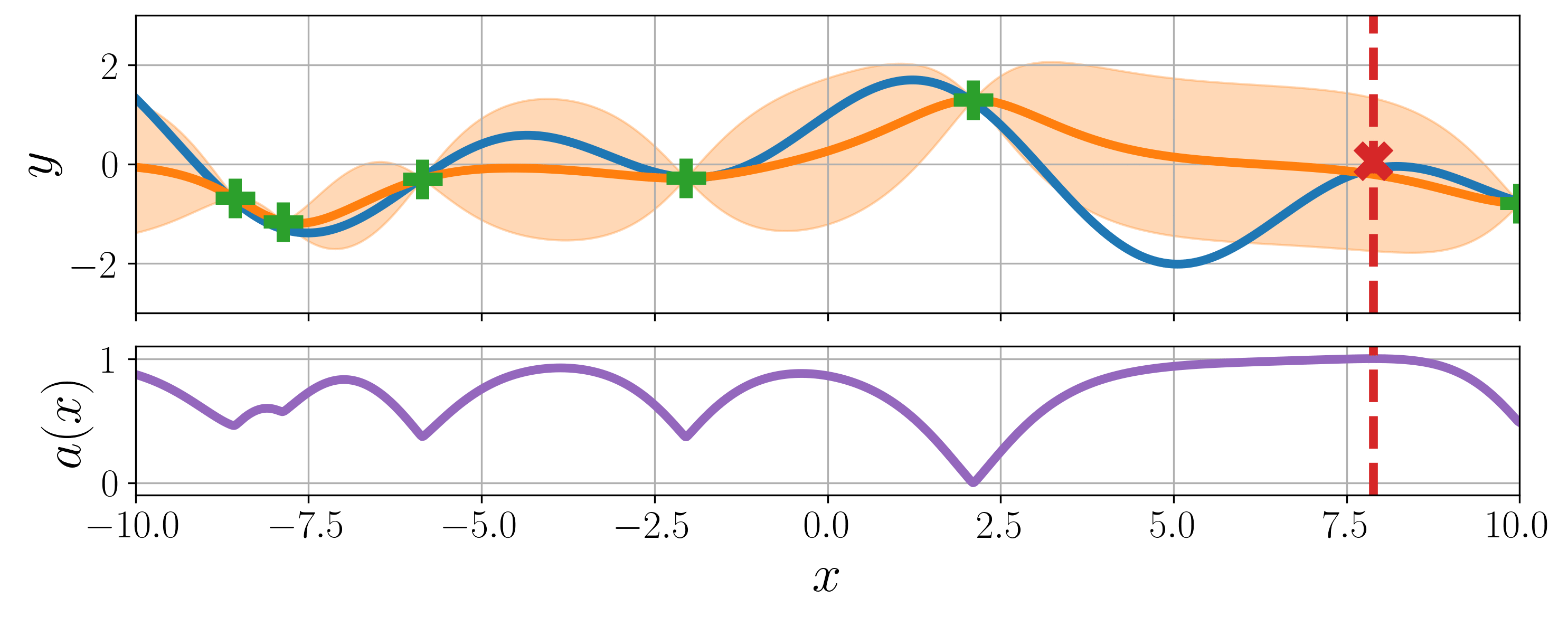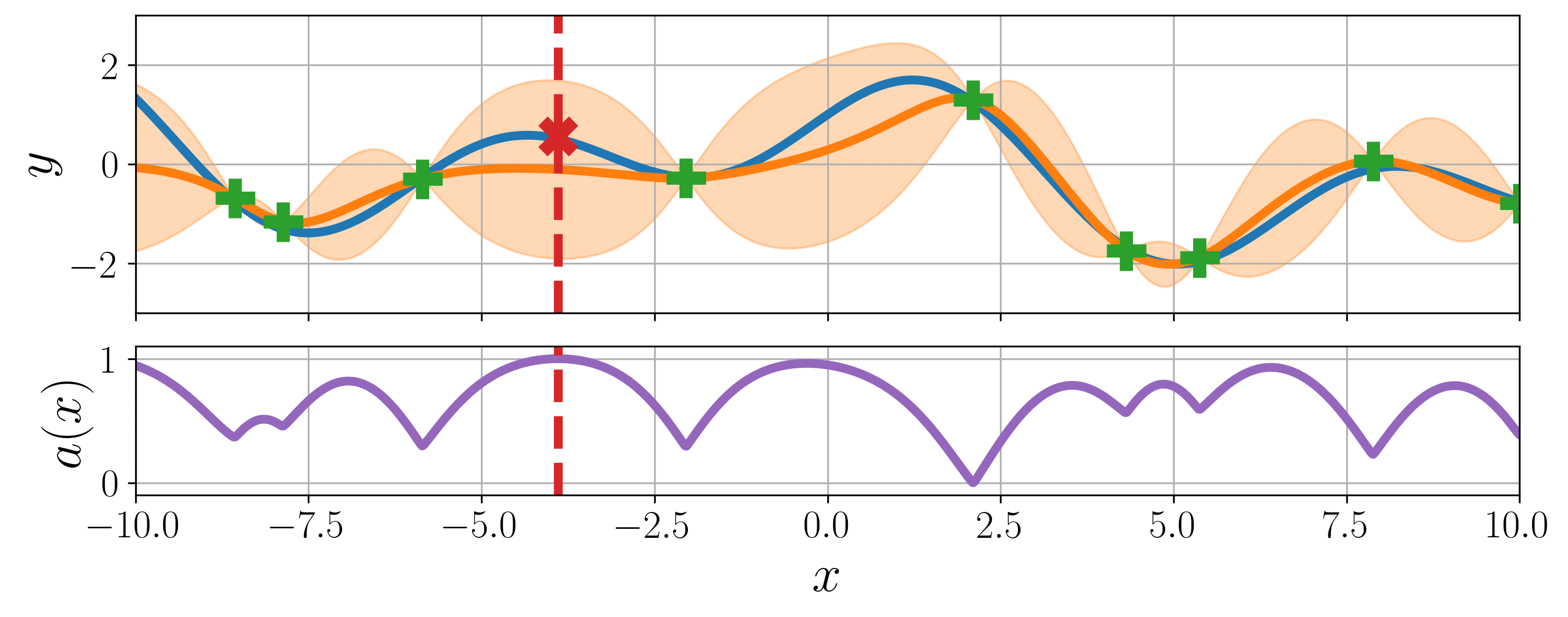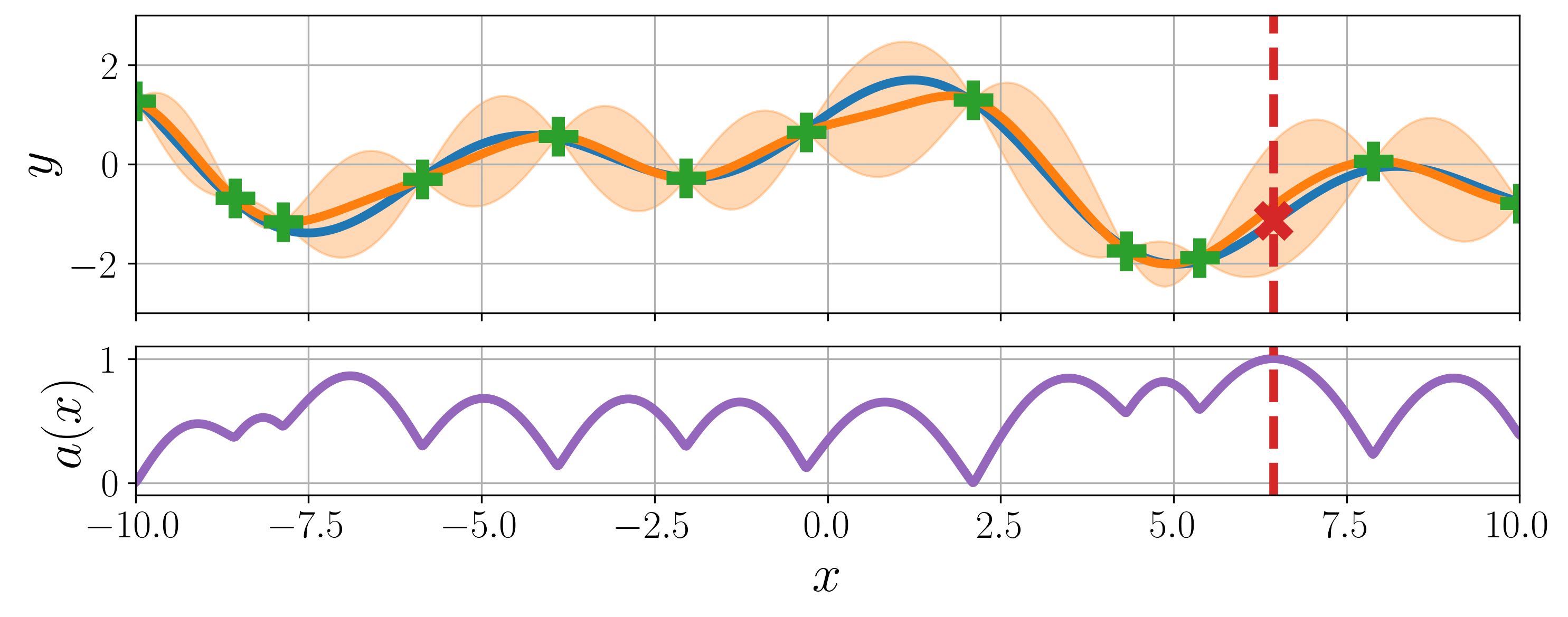
Bayesian optimization is a global optimization strategy for black-box and expensive-to-evaluate functions. Generic Bayesian optimization follows these steps:
Build a surrogate function \(\hat{f}\) with historical inputs \(\mathbf{X}\) and their observations \(\mathbf{y}\), which is defined with mean and variance functions.
Compute and maximize an acquisition function \(a\), defined by the outputs of surrogate function, i.e., \(\mu(\mathbf{x} \mid \mathbf{X}, \mathbf{y})\) and \(\sigma^2(\mathbf{x} \mid \mathbf{X}, \mathbf{y})\).
Observe the maximizer of acquisition function from a true objective function \(f\) where a random observation noise \(\epsilon\) exists.
Update historical inputs \(\mathbf{X}\) and their observations \(\mathbf{y}\) accumulating the maximizer \(\mathbf{x}^{*}\) and its observation \(y\).
This project helps us to execute this Bayesian optimization procedure. In particular, several surrogate functions such as Gaussian process regression and Student-\(t\) process regression and various acquisition functions such as probability of improvement, expected improvement, and Gaussian process upper confidence bound are included in this project.